
第 1 页 / 共 11 页
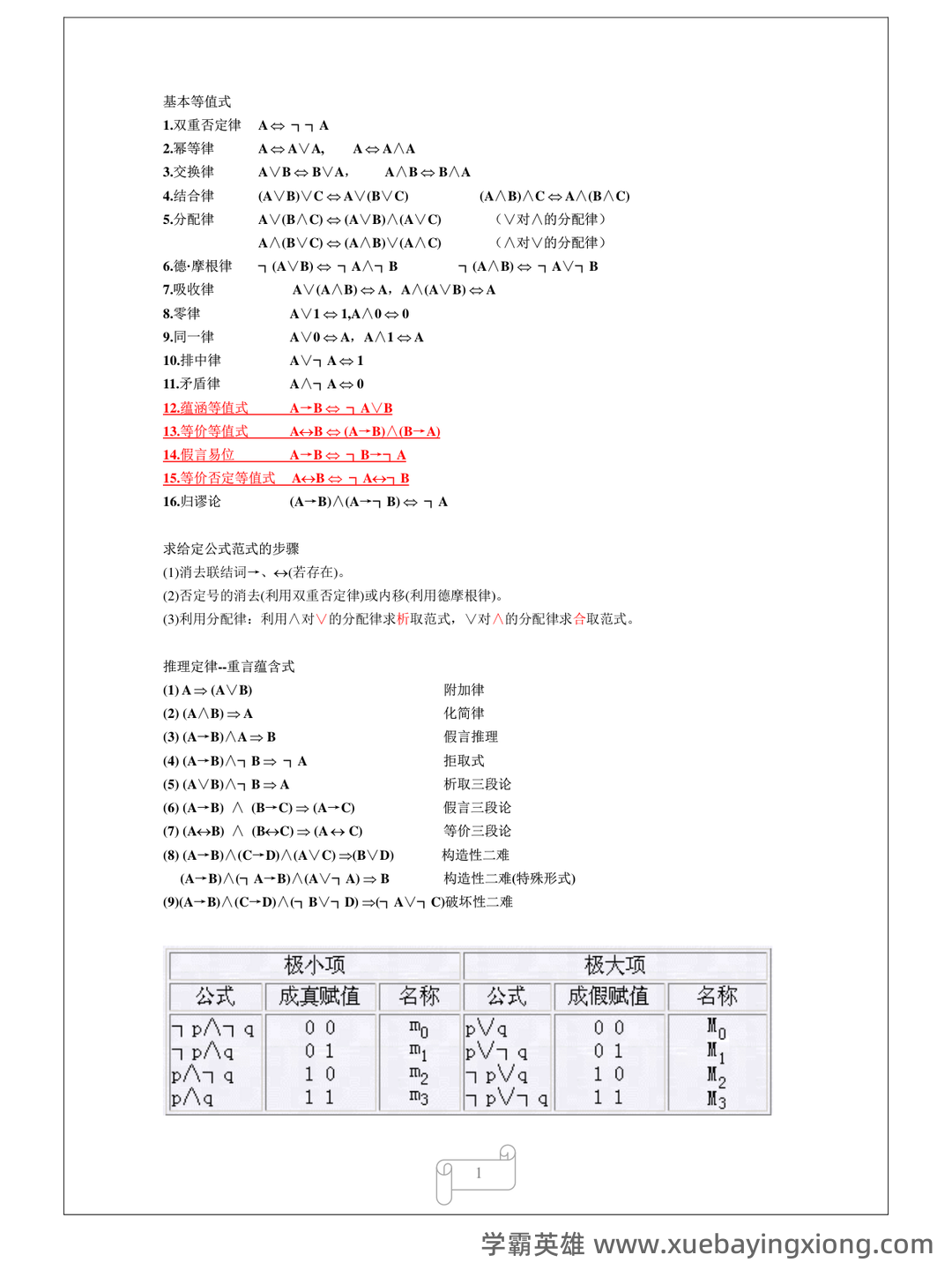
第 2 页 / 共 11 页

第 3 页 / 共 11 页

第 4 页 / 共 11 页

第 5 页 / 共 11 页

第 6 页 / 共 11 页

第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 11 页 / 共 11 页
有哪些重要的离散数学知识点需要掌握?
有哪些重要的离散数学知识点需要掌握? 离散数学,这个看似高深莫测的学科,其实是计算机科学、信息技术等领域基石。想要在这些领域深耕,掌握好离散数学的知识点,就如同掌握了通往未来世界的钥匙。它不仅仅是理论,更是一种思维方式的训练,帮助我们更好地理解和解决复杂问题。 首先,集合论是离散数学的基石。理解集合、子集、并集、交集、补集等基本概念,对于后续学习其他知识点至关重要。“集合论是离散数学的核心,它定义了数学对象之间的一种关系,是理解其他概念的基础。” 深入理解集合运算,能帮助我们更好地进行逻辑推理和问题建模。 接下来是逻辑学,学习命题逻辑、谓词逻辑,以及证明方法,可以有效提高我们的逻辑思维能力。例如,理解“三段论”和“四段论”等常见逻辑形式,能帮助我们构建严谨的论证过程,避免逻辑谬误。 图论也是离散数学中的重要组成部分。学习图的表示方法、图的类型(如有向图、无向图、稀疏图、稠密图等),以及一些基本的图算法,能解决许多实际问题,比如网络设计、社交网络分析等等。 计数原理同样不可或缺。掌握各种计数方法,如排列、组合、二项式定理等,能帮助我们高效地解决求集合元素个数的问题。 “看似简单的计数原理,却能解决许多看似困难的问题。” 最后,关系论值得我们关注。 关系论研究关系的性质,例如对称性、反称性等,能帮助我们更全面地理解对象之间的联系。 掌握这些知识点,对于理解计算机算法、数据库设计以及人工智能等领域都大有裨益。
展开
离散数学
2025-07-30
37次阅读