
第 1 页 / 共 21 页

第 2 页 / 共 21 页

第 3 页 / 共 21 页

第 4 页 / 共 21 页

第 5 页 / 共 21 页

第 6 页 / 共 21 页

第 7 页 / 共 21 页
第 8 页 / 共 21 页
第 9 页 / 共 21 页

第 10 页 / 共 21 页

第 11 页 / 共 21 页

第 12 页 / 共 21 页

第 13 页 / 共 21 页

第 14 页 / 共 21 页

第 15 页 / 共 21 页

第 16 页 / 共 21 页

第 17 页 / 共 21 页

第 18 页 / 共 21 页

第 19 页 / 共 21 页

第 20 页 / 共 21 页

第 21 页 / 共 21 页
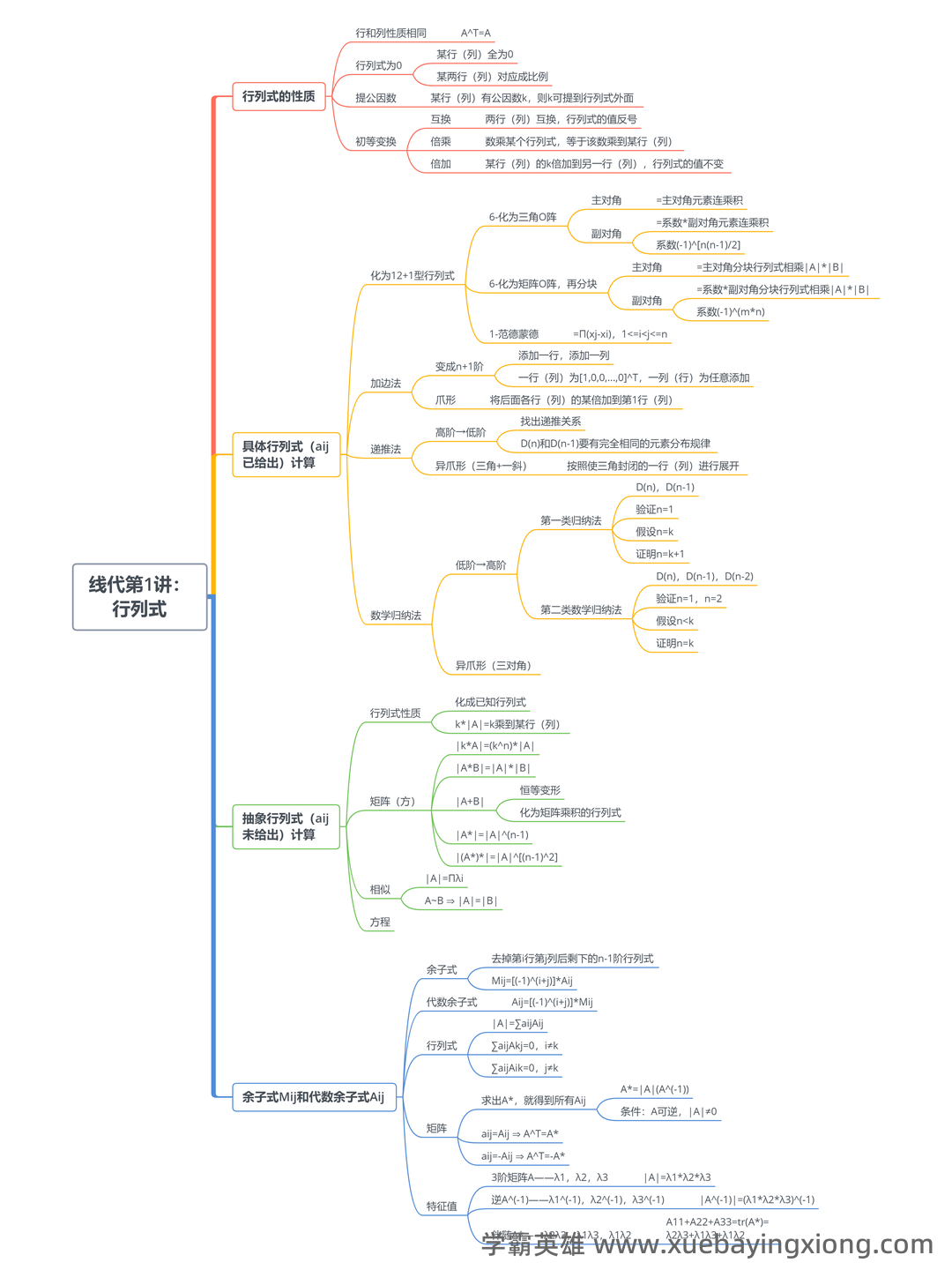
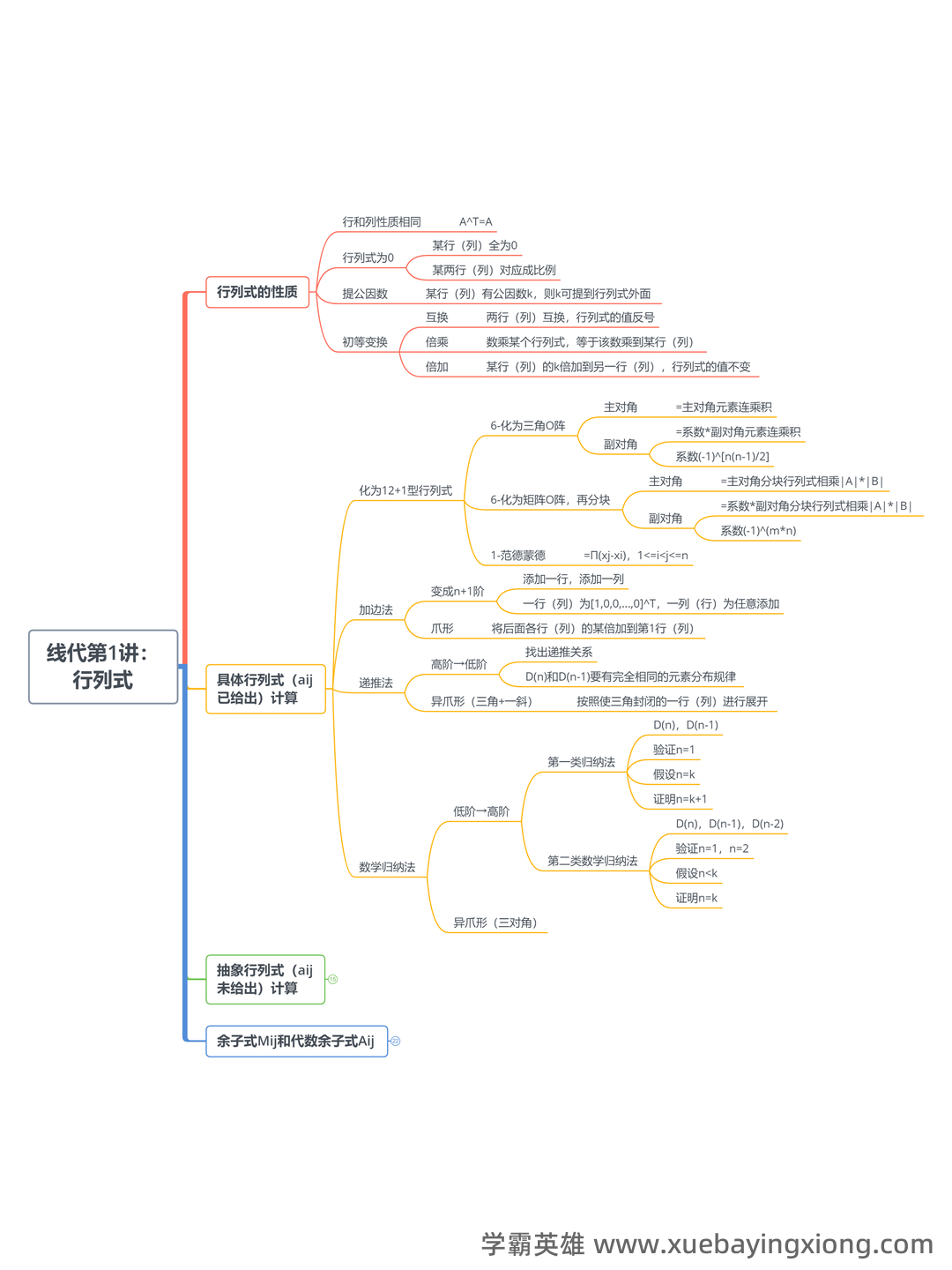
最值得收藏的考研线性代数 重点知识点 思维导图整理
最值得收藏的考研线性代数重点知识点 思维导图整理 线性代数是考研数学中的重要一环,掌握好重点知识点,构建清晰的思维导图,将事半功倍。以下整理了考研线性代数中值得收藏的重点知识点,并以思维导图形式呈现,助力备考。 核心概念与定理 向量空间与线性相关性: 深刻理解向量空间的定义、基和维数。理解向量线性相关的概念,并掌握判断线性相关性的方法。线性相关性是解决线性方程组的基础。 矩阵运算: 矩阵加法、减法、乘法及其性质,共轭矩阵,矩阵的转置。 熟练掌握矩阵乘法运算及其分配律、结合律等重要性质,对后续计算至关重要。 行列式: 行列式的定义、计算方法(如罗伯特·卡尔森法则)、性质以及它与矩阵性质之间的联系。 特征值与特征向量: 深入理解特征值的概念,知道如何求出矩阵的特征值和特征向量。 掌握特征值与矩阵的对角化以及对角化矩阵的性质。 线性方程组的求解: 高斯消元法、克拉默法则,以及这些方法在不同情况下的适用性和优缺点。 思维导图结构建议 (以下为思维导图大致结构,并非具体图形) 中心主题:线性代数 分支1:向量与矩阵 向量空间 线性相关性 矩阵运算 行列式 分支2:特征值与特征向量 特征值 特征向量 矩阵对角化 分支3:线性方程组 高斯消元法 克拉默法则 学习建议 线性代数的理解需要一定的抽象思维能力。建议多做例题,将理论与实际问题联系起来。对于线性方程组的求解,要注重掌握高斯消元法的步骤和技巧。构建自己的思维导图,对知识点进行系统化整理,更有助于理解和记忆。
展开
线性代数
2025-04-19
36次阅读